Ah, recursion. The elegant, powerful, sometimes mind-bending technique that sends shivers down the spines of many a programmer. It's like watching a movie where the ending loops back to the beginning, only slightly different each time. Cool, right? But also, sometimes...confusing.

That was me, not too long ago. I stared at recursive code, trying to untangle the maze of function calls within function calls. My brain felt like it was playing hopscotch through an infinite hallway. Yet, there was an undeniable allure to it. Recursion held the key to solving complex problems in a seemingly magical way.

Then, I stumbled upon the land of dynamic programming. It was like entering a sun-drenched valley after a week in the recursive forest. Everything felt clearer, brighter, more efficient. Dynamic programming offered a structured, step-by-step approach to tackling the same problems that recursion solved with elegant loops and clever memoization.

But how did I get there? My journey wasn't a straight shot. It was a winding path, paved with:

1. Understanding the Power of Recursion:

Imagine a function calling itself. Not once, not twice, but potentially an infinite number of times. That's the magical (and sometimes perilous) world of recursion. It's like solving a puzzle by breaking it down into smaller, self-similar pieces, each piece potentially leading to another self-similar piece.

• a function calls itself until the base cases are reached.

• It breaks down into smaller smaller problem and it route is being trace out.(Its like a tree)

• If the Base Case reached , it store value and then takes it position to back to journey from the trace path.

See how the recursive tree works 👉

Take an example :

function Fib(n) {
  if (n <= 1) { //Base Case
    return n;
  } else {  //recursive case
    return Fib(n - 1) + Fib(n - 2);  
  }
}

2. Grappling with the Recursion Abyss:

But then came the challenges. Stack overflows, infinite loops, the infamous "recursion is hard" meme.

While recursion can be incredibly elegant for certain problems, it has its drawbacks. Stack overflows lurk around every corner, and redundant calculations can slow things down. This is where our hero, dynamic programming, enters the scene.

3. Discovering the Beauty of Dynamic Programming:

Enter dynamic programming. It was like a life raft thrown into my recursive ocean 🌊🌊. Here, instead of blindly trusting the magic 🎇 of self-calls, I could build solutions from the bottom up, storing results in tables to avoid redundant calculations.

Suddenly, problems that took ages to solve recursively became lightning-fast. Fibonacci sequences? Done in a blink. Optimal coin changes? Child's play. Longest common subsequences? Piece of cake (well, almost).

Dynamic Programming: Efficiency Ascendant

Dynamic programming is all about solving problems from the bottom up, storing results along the way to avoid redundant calculations. Think of it like climbing a ladder instead of spiraling down an infinite staircase (ahem, recursion).

But how does recursion relate to all this? Here's the secret handshake:

The Bridge Between Worlds:

1. Breaking Down the Problem: Recursion excels at decomposing problems into smaller, self-similar subproblems. This very act of decomposition reveals the essence of the problem and lays the groundwork for dynamic programming.

2. IdentifyingSubproblem Overlap: As you traverse the recursive tree, you'll start to notice that certain subproblems are solved multiple times. This is where the magic happens!

3. Memoization to the Rescue: Dynamic programming introduces the concept of memoization, which is essentially storing the solutions to subproblems in a table or array. This way, when you encounter the same subproblem again, you can simply look it up in the table and avoid redundant calculations.

From Recursive Roots to DP Blossoms:

Let's take a classic example: the Fibonacci sequence. Calculating the nth Fibonacci number recursively can be beautiful, but it's also inefficient. By understanding the recursive structure and identifying overlapping subproblems, we can easily translate the solution into a dynamic programming approach, storing previously calculated values and achieving lightning-fast results.

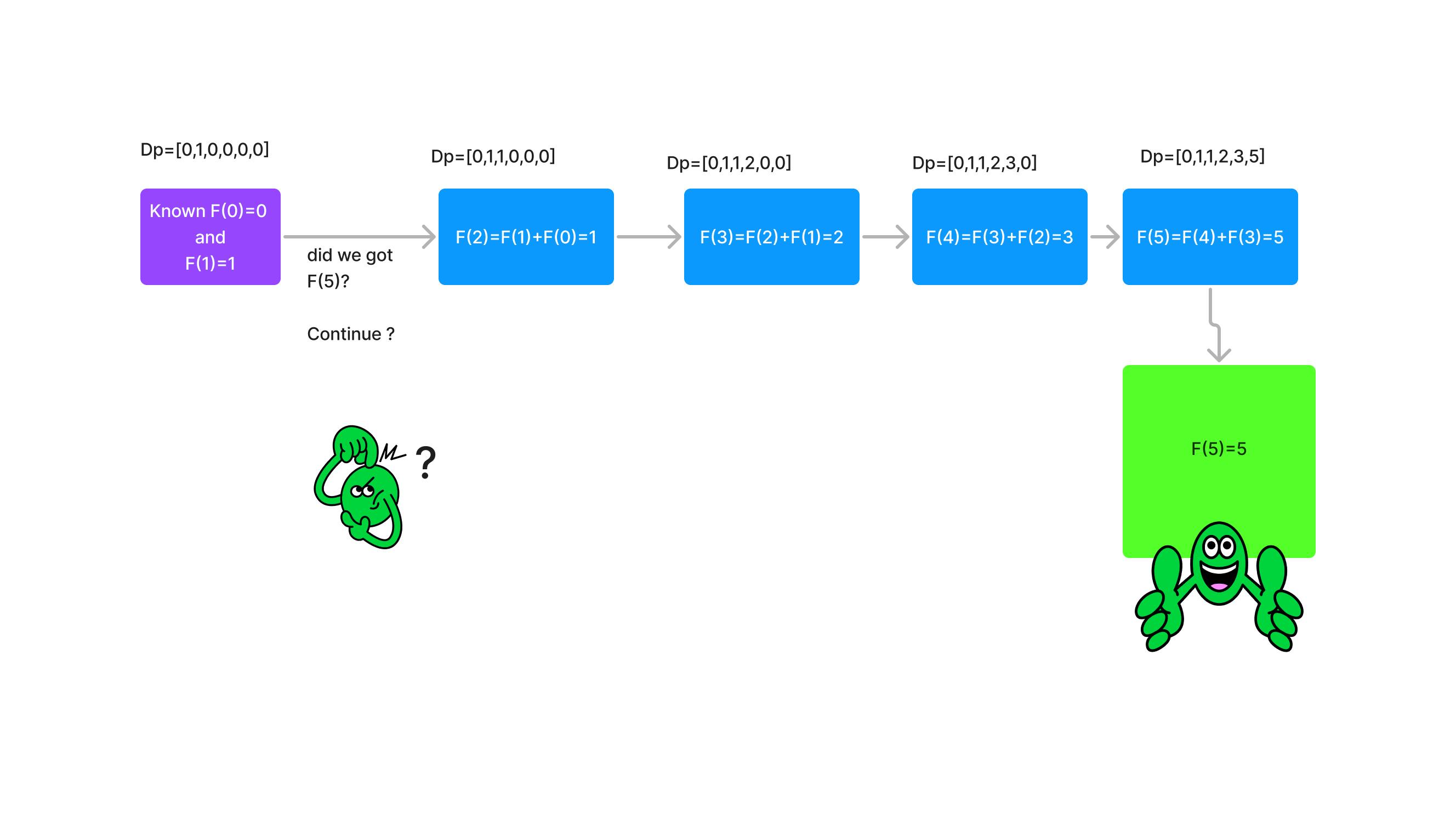
See The example of Fibonacci F(n)=F(n-1)+F(n-2)

for F(5) = 5 and series should be , (0,1,1,2,3,5)

function fibonacci(n)
    {

        let f = new Array(n+2); // 1 extra to handle case
        let i;
        /* 0th and 1st number of the series are 0 and 1*/
        f[0] = 0;
        f[1] = 1;
        for (i = 2; i <= n; i++)
        {
            /* Add the previous 2 numbers in the series
            and store it */
            f[i] = f[i-1] + f[i-2];
        }
        return f[n];
    }

The Benefits of Bridging the Gap:

So, why is understanding the connection between recursion and dynamic programming important? Here are a few reasons:

• Deeper Problem Understanding: By seeing how recursion breaks down problems and how dynamic programming builds solutions efficiently, you gain a deeper understanding of the problem itself.

• Flexibility and Choice: You can choose the best approach for the specific problem at hand. Sometimes recursion might be easier to understand, while dynamic programming offers superior efficiency.

• Problem-Solving Toolbox Expansion: You add both powerful techniques to your problem-solving arsenal, becoming a more versatile and adaptable programmer.

Remember:

So, dear reader, if you're on your own journey from recursion to dynamic programming, don't despair. Embrace the challenges, celebrate the moments of clarity, and enjoy the satisfaction of mastering these remarkable tools. And remember, the path, both confusing and illuminating, is just as valuable as the destination.

💡💡Think you've mastered recursion? Try solving these real-world problems using DP and see how efficient you can get!

#dp #recursion #dsa #problem-solving #creativity